NEPHROID
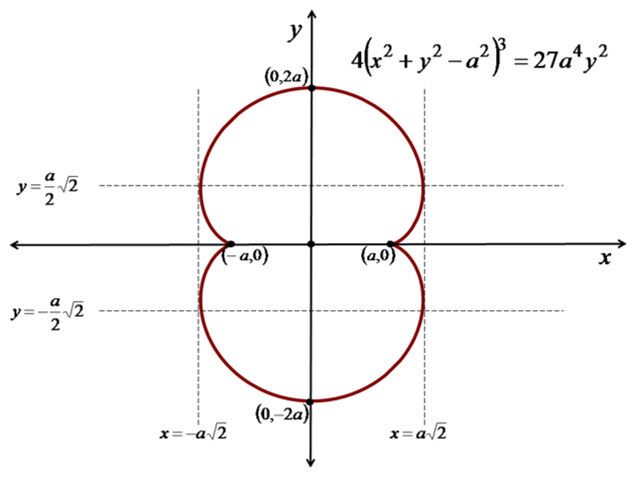
The Nephroid is one of the curves from a family of curves called Epicycloids and is formed when one circle rolls around the outside of another. It turns out that if the radius of the rolling circle is ½ of the radius of the stationary circle, a point on the rolling circle traces a Nephroid. Nephroid means kidney-shaped. More details about this curve can be found in my book Playing With Dynamic Geometry, Chapter 7.
There are many different geometric constructions involving the Nephroid and, over time, I will use a lot of them. The animations presented below are presented in pairs. The first of the pair is a basic construction that either generates the Nephroid or demonstrates one of its properties. The second of the pair is my “artistic” rendering based on the construction found in the first of the pair, but with the mathematical information hidden.
There are many different geometric constructions involving the Nephroid and, over time, I will use a lot of them. The animations presented below are presented in pairs. The first of the pair is a basic construction that either generates the Nephroid or demonstrates one of its properties. The second of the pair is my “artistic” rendering based on the construction found in the first of the pair, but with the mathematical information hidden.