Deltoid
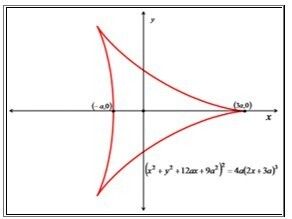
The graph of the curve to the left, shown with its equation, is called the Deltoid. Conceived by Leonhard Euler in 1745, the Deltoid (sometimes called the Tricuspoid) was studied in connection with caustic curves (i.e., the reflection or refraction of light). It was also investigated by Steiner in 1856 and is sometimes called Steiner's Hypocycloid. In point of fact, the Deltoid is a member of a family of curves called Hypocycloids. This variety of cycloid is obtained as the locus of a point attached to the circumference of one circle rolling along the circumference of another circle, but rolling interior to it. The Deltoid is the specific Hypocycloid where the radius of the fixed circle is three times as large as the radius of the rolling circle.
The animations below are presented in pairs. The first of the pair is the basic geometric construction that either generates the Deltoid or demonstrates one of its properties. The second of the pair is my “artistic rendering” based on the first of the pair.
The animations below are presented in pairs. The first of the pair is the basic geometric construction that either generates the Deltoid or demonstrates one of its properties. The second of the pair is my “artistic rendering” based on the first of the pair.