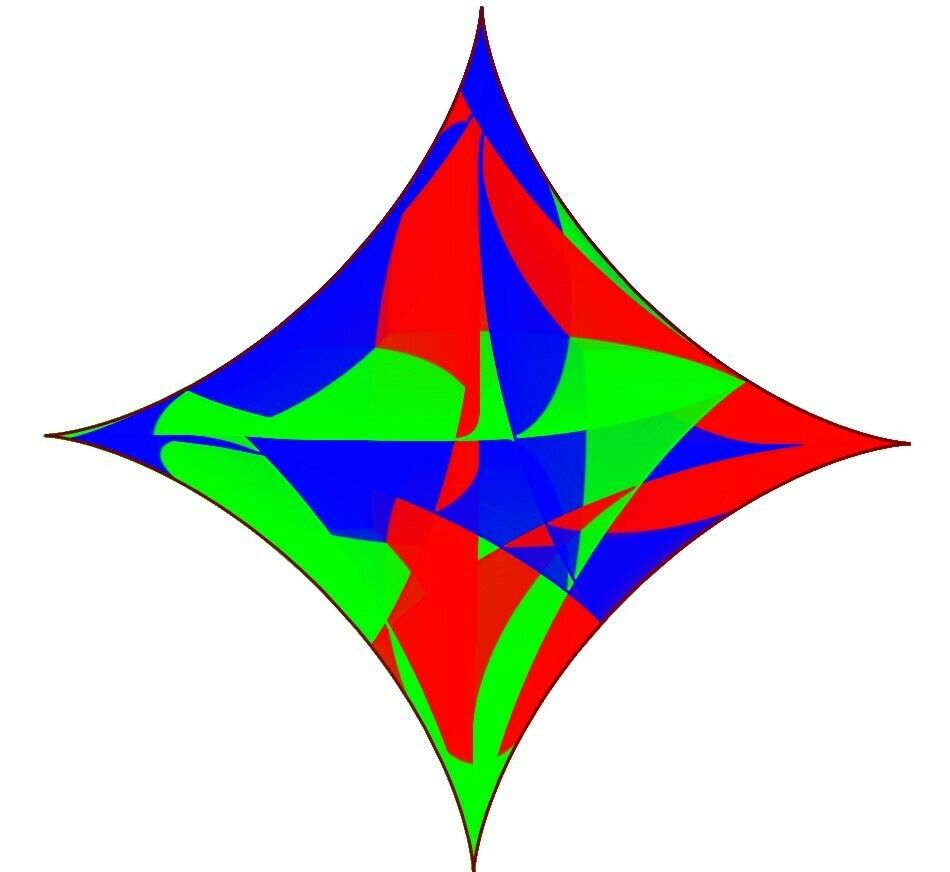
Astroid
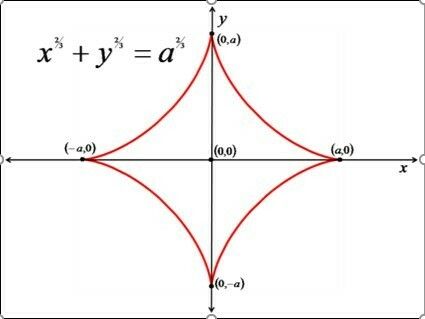
The curve called the Astroid is shown to the left with its algebraic equation. Astroid (also sometimes referred to as the tetracuspid), of course, means star-shaped. More details about this curve can be found in my book Playing with Dynamic Geometry, Chapter 11.
There are many different geometric constructions for the Astroid (and over time, I will use a lot of them). The animations below are presented in pairs. The first of the pairs is the basic geometric construction that either generates the Astroid or demonstrates one of its properties. The second of the pairs is my “artistic” rendering based on that basic construction.
There are many different geometric constructions for the Astroid (and over time, I will use a lot of them). The animations below are presented in pairs. The first of the pairs is the basic geometric construction that either generates the Astroid or demonstrates one of its properties. The second of the pairs is my “artistic” rendering based on that basic construction.